Un pequeño repaso de algunos objetos y conceptos
Para ahondar un poco en la posibilidad de construcción de sonidos a través de Pd, he decidido repasar en este post algunos de los conceptos y objetos relacionados con la síntesis aditiva.
Si tenemos un generador de ondas sinusoidales, vamos a generar un sonido con sólamente una frecuencia. Es un sonido realmente simple y nos permite la creación de diversos sonidos si usamos varios de estos, pero sobre esta idea regresaremos más adelante, por ahora examinemos las propiedades de una onda sinusoidal.
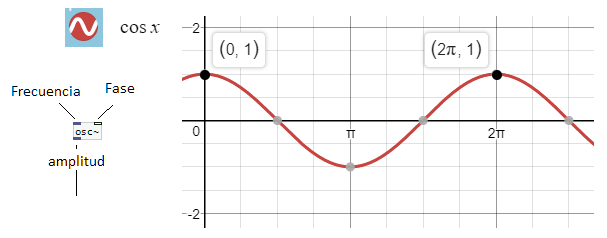
En el gráfico anterior, podemos observar una onda cosinusoudal (tiene la misma forma de la sinusoidal, pero no comienza su periodo en cero sino en uno). El primer parámetro que nos interesa controlar de este tipo de onda es su frecuencia.
La frecuencia la podemos entender como la cantidad de veces que cumple un ciclo por segundo. En el gráfico podemos observar a la onda en color rojo comenzando un ciclo a la izquierda y terminándolo en la línea punteada. La cantidad de veces que eso ocurre por segundo es lo que podemos percibir como una altura. En Pd el objeto que se encarga de producir este tipo de onda es |osc~|. Tal como aparece en el gráfico, la frecuencia puede ser controlada a través de la entrada izquierda y tenemos la posibilidad de enviarle datos o audio (tema que expandiremos en una publicación posterior).
El segundo parámetro que nos interesa por el momento es la intensidad. La intensidad en el gráfico es representada por el eje vertical y lo pensamos como la amplitud, que tan amplio es el movimiento de la onda en este eje en cada instante. Traducido a sonido esto es lo que percibimos como intensidad o volumen. Por defecto, el objeto |osc~| genera la máxima amplitud, es decir 1, lo cual va a producir una onda cuya amplitud oscila entre 1 y -1, de la misma forma que los datos que salen del objeto |osc~|.
Los dos parámetros pueden ser pensados como valores fijos o podemos hacerlos variar en el tiempo. No voy a darle preferencia a ninguno de los dos, pues pienso que ambos tienen un potencial sonoro interesante.
Primero voy a examinar la posibilidad de variación de la intensidad.
Los gráficos a, b y c nos muestran un periodo de una onda cosinusoidal, pero cada una de ellas tiene una intensidad diferente. Si deseamos darle una intensidad constante a una onda sinusoidal en Pd, sólo debemos multiplicar la salida del oscilador por una constante, ya sea a través de la inicialización del objeto (e.g. |*~ 0.7|), a través del envío de un mensaje o el envío de información con una caja numérica.
Si la información que enviamos a esa multiplicación varía en el tiempo también lo hará la intensidad de la onda sinusoidal. Sólo debemos considerar las diferentes situaciones en las que se pueden dar esos cambios para hallar su uso posible.
En este gráfico podemos apreciar el cambio en el tiempo de una onda sinusoidal. En este caso es sonido cuya intensidad es constante al comienzo y luego pasa por un momento de ascenso y posterior al instante de llegada a la máxima intensidad, decrece hasta desaparecer. Esa descripción del comportamiento de la intensidad en el tiempo es lo que llamaremos envolvente. En Pd esta envolvente puede ser creada mientras suena la onda sinusoidal y nosotros cambiamos la intensidad manualmente, sin embargo, si queremos crear una envolvente detallada no tiene mucho sentido hacerlo así, es mejor automatizar la creación de tal envolvente.
Realizar esto es realmente sencillo, basta con enviar un mensaje a un generador de rampas |line~| con los datos que deseamos para crear nuestra envolvente.
En este ejemplo, podemos encontrar diversos mensajes que le podemos enviar a |line~|. Contemplemos primero una situación en la cual asumimos que el valor inicial de la intensidad es cero. El primer mensaje |0, 1 3000<, producirá un ascenso lineal en la intensidad entre 0 y 1 durante 3000 milisegundos, lo cual percibiremos como un sonido que aparece lentamente durante tres segundos.
En el caso del segundo mensaje |0, 1 50<, la intensidad cambia rápidamente entre 0 y 1, 50 milisegundos es la vigésima parte de un segundo, por tanto sentiremos ese ascenso de la intensidad de alguna forma similar a un sonido percutido o pulsado.
El tercer mensaje, produce un salto inmediato de 0 a 1, eso producirá un "pop" (onomatopeya para describir el resultado en los parlantes), si pensamos en los datos que salen del oscilador (que son 44100 por segundo por defecto) viene una cadena de ceros y de repente aparece un 1 (0 0 0 0 0 0 0 0 1) eso traducido por |dac~| sería como tener 0 voltios y de repente enviar toda la corriente, ese cambio repentino en la membrana del parlante se traduce en ese ruido característico. Ahora, luego de ese cambio repentino, durante 5 segundos (5000 milisegundos) el sonido disminuirá su intensidad hasta desaparecer. Existe una situación relacionada a los cambios repentinos, y es la relación con la fase. Aquí abro un paréntesis corto para explicarlo.
La fase en un generador de ondas sinusoidales es un mensaje que reinicia el periodo, pero desde un punto específico, por ejemplo, si retornamos al primer gráfico y dividimos en cuatro partes iguales el primer periodo, obtendremos cuatro puntos. El primero corresponde a la fase cero (0) en el cual el valor de amplitud es uno (1); el segundo valor para la fase (0.25 o 1/4) tiene un valor de intensidad cero (0); el tercer valor (2/4 o 0.5) tiene un valor en su amplitud de -1; el cuarto (0.75 o 3/4) un valor de cero (0) nuevamente.
La entrada de fase en un objeto |osc~| está a la derecha. Si enviamos un valor de 0.25 o de 0.75 a tal entrada al tiempo con el envío del mensaje que tiene un cambio abrupto (de cero a uno) no se producirá el "pop" porque se está multiplicando por uno un valor que viene en ascenso hacia la intensidad máxima.
Retornando a los mensajes que entran a |line~|, el cuarto mensaje se comporta igual al anterior, sólo que el descenso no tomará 5 segundos, sino una vigésima parte de un segundo, estará en el límite de percepción, será un sonido realmente corto.
Los siguientes dos mensajes (cero y uno) harán que el valor cambie abruptamente a esos valores y permanezca constante. El caso siguiente es un poco diferente, al sólo tener dos valores, le dirá a |line~| que a partir del valor que tenga en el momento haga una rampa (en la dirección que sea) hacia 0.5 en 400 milisegundos y cuando termine quedará constante en ese valor.
Para controlar el comportamiento, de una forma similar al gráfico de envolvente (gris y azul), sólamente es necesario activar en diferentes momentos mensajes que moldeen la intensidad del sonido tal como se requiera.
Hasta ahora sólo hemos hablado de un oscilador, pero ¿Qué ocurre cuando tenemos varios al mismo tiempo?
Supongamos que tenemos dos osciladores cuya relación de frecuencias es 1:2, osea la segunda es el doble que la primera. En ese caso tendríamos lo siguiente:
Al sumar el resultado de los dos generadores de ondas sinusoidales obtenemos una nueva forma de onda, y esto se traduce en lo que reconocemos como timbre. También se desprenden diversas situaciones de esta simultaneidad de sonidos.
1- Cuando la relación de frecuencias es muy cercana, la interacción de las frecuencias produce desde fenómenos de interferencia que se perciben como cambios lentos de intensidad si son muy cercanas y salen por el mismo parlante.
2- Cambio de espacialización cuando las frecuencias son muy cercanas y salen por dos parlantes diferentes.
3- Frecuencia diferencial, es decir, la resta de las frecuencias produce un componente de frecuencia grave, posteriormente volveremos sobre este tema (en otro post).
4- Si cambiamos la intensidad en el tiempo de los dos osciladores producimos un timbre cambiante en el tiempo.
5- Si la intensidad tope de uno de los osciladores es mayor que la del otro, percibimos como principal la más fuerte.
De esta última, podemos extraer también algo escencial en la creación de timbres a través de esta técnica (síntesis aditiva). Si tenemos muchos osciladores, no sólo dos, podemos crear sonidos con una mayor complejidad. Por complejidad quiero referirme a la forma de la onda. En el gráfico de la suma de sinusoides observamos que el resultado es una onda con una forma un poco más compleja. Al sumar varias y cuyas relaciones de frecuencia incluso se desvíen de una relación entera, podemos crear formas de onda realmente complejas.
La pregunta entonces sería ¿Qué pensar cuando queremos crear un timbre (sonido particular) de esta forma?
Lo primero es determinar si se desea un sonido con una relación armónica o no, es decir, por relación armónica me refiero a que cada uno de los osciladores entra una frecuencia que tiene una relación entera con la del primero, lo que equivale a multiplicar esa frecuencia por números enteros. No siempre se va a percibir como un sonido de gran armonicidad, eso también depende de las intensidades que le demos a cada oscilador y si sus frecuencias son múltiplos cercanos a la fundamental. Para ilustrar esto, es un buen ejercicio replicar el siguiente patch y jugar un poco con las intensidades y posteriormente cambiar el factor en las multiplicaciones.
A cada uno de esos osciladores cuya frecuencia es un múltiplo de la frecuencia que se marca como fundamental (a los cuales también llamamos componentes), es posible modificarle el multiplo en el tiempo, además, darle un comportamiento dinámico único. Hacer este tipo de procesos puede influir fuertemente en la configuración tímbrica que estemos construyendo. 
Comentarios
Publicar un comentario